1936: 排座位
Description
【题目描述】
同学们在教室中坐成了M行N列,有D对同学上课时会交头接耳。坐在第i行第j列的同学的位置是(i,j),为了方便同学们进出,在教室中设置了K条横向的通道,L条纵向的通道。
班主任打算重新摆放桌椅,改变同学们桌椅间通道的位置,因为如果一条通道隔开了两个会交头接耳的同学,那么他们就不会交头接耳了。
试编程给出最好的通道划分方案,使上课时交头接耳的学生对数最少。
【输入格式】
输入的第1行有5个整数,分别是M、N、K、L、D(2≤N,M≤1000,0≤K≤M,0≤L<N,D≤2000)
接下来D行,每行有4个用空格分隔的整数,第i行的4个整数xi、yi、pi、qi,表示坐在位置(xi、yi)与(pi、qi)的两个同学会交头接耳(输入时保证他们前后相邻或者左右相邻)。
输入数据需保证最优方案的唯一性。
【输出格式】
输出共两行。
第一行包含K个整数,a1,a2,……,aK,表示第a1行和a1+1行之间、第a2行和第a2+1行之间、…、第aK行和第aK+1行之间要开辟通道,其中ai< ai+1,每两个整数之间用空格隔开(行尾没有空格)。
第二行包含L个整数,b1,b2,……,bk,表示第b1列和b1+1列之间、第b2列和第b2+1列之间、…、第bL列和第bL+1列之间要开辟通道,其中bi< bi+1,每两个整数之间用空格隔开(行尾没有空格)。
【输入样例】
4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4
【输出样例】
2
2 4
Input
第一行,有5个用空格隔开的整数,分别是M,N,K,L,D(2<=N,M<=1000,0<=K<M,0<=L<N,D<=2000)。
接下来D行,每行有4个用空格隔开的整数,第i行的4个整数Xi,Yi,Pi,Qi,表示坐在位置(Xi,Yi)与(Pi,Qi)的两个同学会交头接耳(输入保证他们前后相邻或者左右相邻)。
输入数据保证最优方案的唯一性。
Output
共两行。
第一行包含K个整数,a1a2……aK,表示第a1行和a1+1行之间、第a2行和第a2+1行之间、…、第aK行和第aK+1行之间要开辟通道,其中ai< ai+1,每两个整数之间用空格隔开(行尾没有空格)。
第二行包含L个整数,b1b2……bk,表示第b1列和b1+1列之间、第b2列和第b2+1列之间、…、第bL列和第bL+1列之间要开辟通道,其中bi< bi+1,每两个整数之间用空格隔开(行尾没有空格)。
Sample Input Copy
4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4
Sample Output Copy
2
2 4
HINT
【输入输出样例解释】
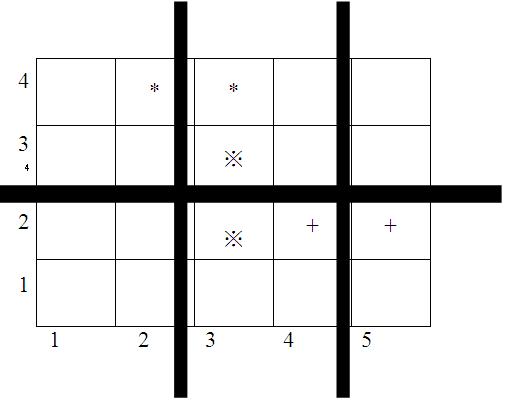
上图中用符号*、※、+ 标出了3对会交头接耳的学生的位置,图中3条粗线的位置表示通道,图示的通道划分方案是唯一的最佳方案。